Clustering Methods
Clustering, like dimension reduction is a form of unsupervised learning. They are both used to divide the data set into smaller groups so that it can be better understood. Cluster analysis was first used in baseball against the Hall of Famer Ted Williams. If you didn’t know Ted was a lefty and he was very apt to pulling the ball. Enough so that teams started moving their infielders around to block the holes that he regularly exploited. This was around a hundred years ago, they didn’t have any type of software that told everyone what pitch was thrown, how fast it was, where it was thrown, what the count was, and the precise location that the batter hit the ball. With this information teams have now started to shift on almost every single pitch and they should because cluster analysis shows them the batters tendencies. If you know you’re about to throw an inside fastball and you know the lefty tends to pull that pitch into the 3-4 hole why wouldn’t you position your team to make that an out. The pitchFx technology in every team’s stadium makes finding tendencies like this extremely easy with one query, which is basically like clustering except you need to already know by which information you want to divide the data set. So if you already know how you’re going to pitch someone with Pitch Sequencing you can easily figure out before a game where you want your fielders to stand for each pitch and then you have yourself a strategy that only luck can beat. To show you how clustering works I first need to grab data from a database in SQLite which is really cool because now you’ll be able to run algorithms on queried reports that you created in SQL. You aren’t very likely to learn something like this in a class because it uses two different programs and a class generally only focuses on one so hopefully this makes sense and you learn something new.
Connecting to an SQLite Database
#First you will need the RSQLite package which enables you to run SQLite queries inside of R or RMarkdown which is what I am making this website in.
require(RSQLite)## Loading required package: RSQLite#Next you have to connect to the database.I named my database MLBData.db
conn=dbConnect(RSQLite::SQLite(),"MLBData.db")
#Finally you run your query by selecting what data you want, from which tables and how you would like that information grouped or ordered.
conn## <SQLiteConnection>
## Path: C:\Users\jtvan\Documents\MachineLearningWebsite\MLBData.db
## Extensions: TRUEdata=dbGetQuery(conn,"select PlayerID,Player.Team,Player.POS, Salaries.Salary,Age, Batting2019.*
from Player
join Salaries on Salaries.Name=Player.Name
join Batting2019 on Batting2019.Name=Player.Name")
#As you can see, we now have a dataset comprised of three different tables in an SQLite database. The method is similar if you would like to use an SQLite database in a python.
head(data)## PlayerID Team POS Salary Age Name year PA HR
## 1 375 Los Angeles Angels 1B 28000000 40 Albert Pujols 2019 545 23
## 2 282 Detroit Tigers 1B 30000000 37 Miguel Cabrera 2019 549 12
## 3 816 Texas Rangers C 3250000 37 Jeff Mathis 2019 244 2
## 4 826 Texas Rangers LF 21000000 37 Shin-Soo Choo 2019 660 24
## 5 760 St. Louis Cardinals C 20000000 37 Yadier Molina 2019 452 10
## 6 525 New York Mets 2B 24000000 37 Robinson Cano 2019 423 13
## Krate BBrate OBPS SB b_ab_scoring b_swinging_strike b_total_swinging_strike
## 1 12.5 7.9 0.734 3 136 169 928
## 2 19.7 8.7 0.744 0 111 246 1008
## 3 35.7 6.1 0.433 1 45 179 488
## 4 25.0 11.8 0.826 15 108 335 1149
## 5 12.8 5.1 0.711 6 105 171 903
## 6 16.3 5.9 0.736 0 81 155 790
## xba xslg xwoba xobp xiso ExitVelocity LaunchAngle sweet_spot_percent
## 1 0.253 0.433 0.319 0.316 0.175 88.3 12.4 26.7
## 2 0.273 0.443 0.332 0.340 0.167 90.3 12.2 38.5
## 3 0.166 0.226 0.196 0.216 0.058 85.7 16.8 29.6
## 4 0.260 0.469 0.356 0.368 0.206 91.3 8.7 32.1
## 5 0.275 0.443 0.325 0.319 0.165 87.4 13.8 42.1
## 6 0.280 0.450 0.328 0.330 0.167 90.8 7.3 33.6
## barrel_batted_rate SolidContactP HardHitP z_swing_percent SwingP OZ_Swing%
## 1 6.0 3.7 36.3 59.7 11.1 30.8
## 2 6.4 7.2 44.6 67.8 14.7 34.0
## 3 1.4 3.5 26.4 68.6 30.6 34.1
## 4 8.8 9.0 49.0 63.9 20.9 20.1
## 5 3.8 7.4 34.7 75.3 14.9 38.0
## 6 7.4 6.2 46.0 74.1 11.0 35.6
## out_zone_swing_miss OutZoneSwingP ContactP in_zone_swing WhiffP batted_ball
## 1 100 332 88.9 576 18.2 431
## 2 151 371 85.3 632 24.4 390
## 3 77 154 69.4 327 36.9 142
## 4 151 270 79.1 860 29.5 399
## 5 84 316 85.1 564 19.0 366
## 6 99 283 89.0 507 19.6 324
## pop_2b_sba pop_3b_sba exchange_2b_3b_sba maxeff_arm_2b_3b_sba Speed
## 1 22.5
## 2 23.5
## 3 2.12 1.72 0.76 76.6 25.8
## 4 26.6
## 5 1.98 1.45 0.68 84.1 22.8
## 6 24.7dbDisconnect(conn = conn)The end goal for clustering is to find variables or hitting statistics that result in players getting paid more or less. Clearly we don’t want to use pitcher’s information so I will write a new query that creates the data set without pitchers. I will also exclude catchers because they should be valued based on things like pitch framing ability and pop up time. It also needs to be noted that I am only using two different clustering techniques and there are way more than two ways to divide data sets.
Agglomerative Hiearchical Clustering
Hierarchical clustering has two approaches: agglomerative or divisive. Agglomerative is a “bottom up” approach, starting with individual points and merging the closest clusters until all are combined into one cluster. Divisive is the opposite - a “top down” approach, starting with all in one cluster and then splitting until the clusters contain only one point each. Agglomerative clustering is much more common, so I will be using this method for hierarchical clustering.
Agglomerative clustering can find the proximity between points using three methods: single link, complete link, and group average. Single link defines proximity as the distance between the closest two points in different clusters. Complete link defines it as the distance between the two farthest points in different clusters. Group average defines proximity as the average pairwise proximities of all pairs of points from different clusters. I will be using a complete link because their are a ton of variables meaning there will most likely be a large difference between points.
## Loading required package: cluster## [1] 240 41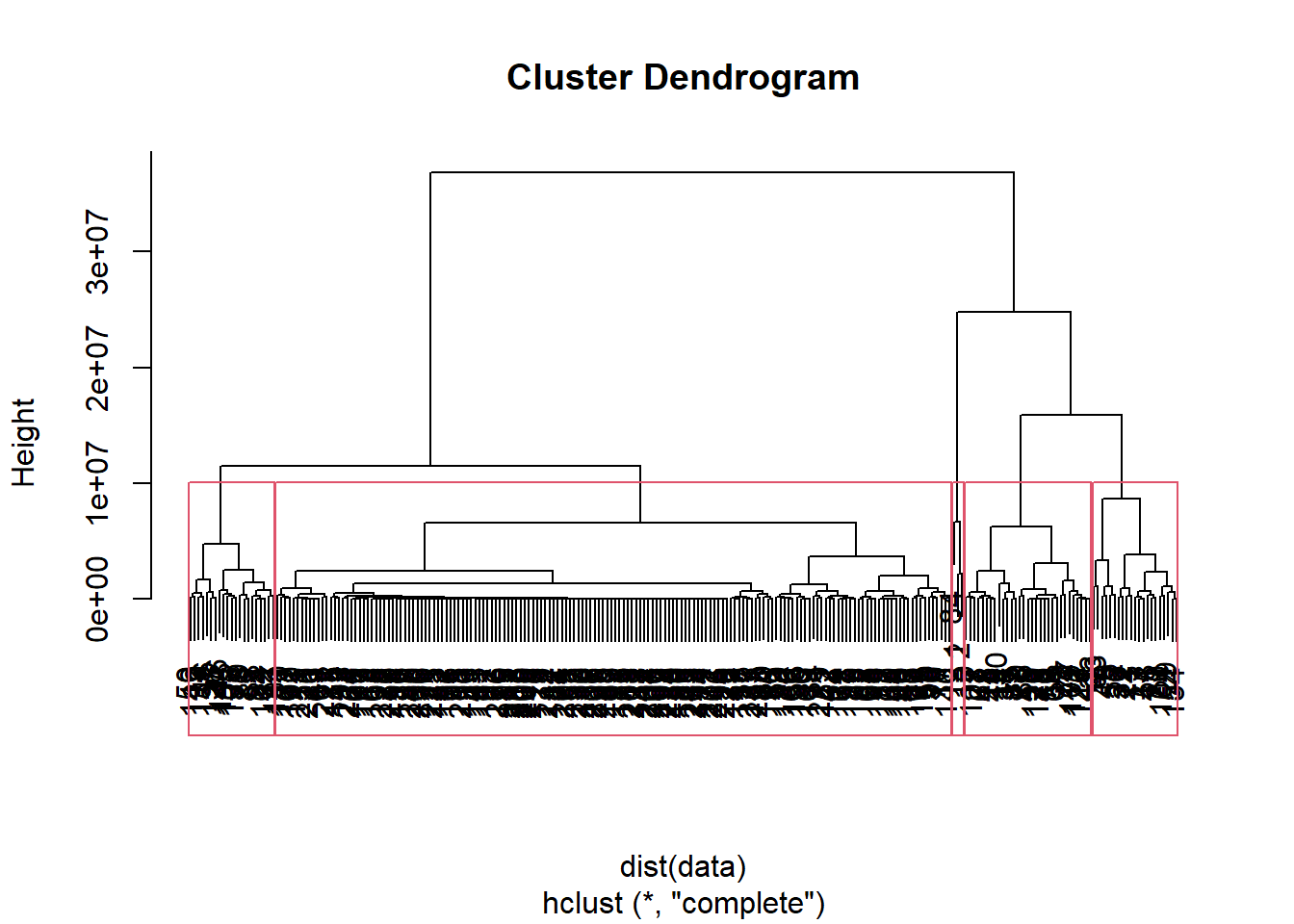
## [1] 1 1 2 2 2 3 4 4 5 4 2 4 3 3 2 5 3 4 5 2 2 4 2 5 3 2 2 4 2 4 5 2 4 3 3 3 3
## [38] 4 3 2 4 3 4 4 4 5 5 4 4 5 3 2 2 2 4 3 5 4 3 3 3 3 3 4 3 3 4 3 3 3 2 3 2 3
## [75] 3 4 4 5 4 3 3 3 3 1 3 4 4 5 5 3 3 5 2 3 3 3 3 3 3 3 3 5 3 2 3 3 4 5 4 3 3
## [112] 4 3 3 3 3 3 3 3 4 3 3 3 3 4 5 3 4 3 3 3 3 5 5 3 3 5 3 3 3 3 5 5 3 3 3 3 3
## [149] 3 3 3 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
## [186] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
## [223] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3## clust5
## 1 2 3 4 5
## 3 21 164 31 21As you can see above, the 240 players have been divided into five groups. Normally this dendogram would result in someone choosing to separate the data into four groups because if I cut the graph at the greatest tree length I would get four groups. I decided on five because I was interested in seeing the difference between clusters five and three. The group with only three players can be seen as outliers because they aren’t very similar to any other group that has at least 20 players. The next step would be to analyze each cluster but first we will look at another method of clustering.
DBSCAN
DBSCAN is a density-based clustering method that locates the areas of the data where there is high density. It separates the high density from the low density areas and clusters based off of that. Now density can be subjective but this algorithm uses what is called a specified radius, Eps, of a data point and estimates the density based on the number of points within the specified radius. This method is also more than capable of handling noise within the data as well as clusters that are arbitrary shapes and sizes. This makes DBSCAN, in this regard, more accurate than K-means. It finds clusters that K-means might not find and I know i didn’t talk about K-means clustering in this website but just know it’s another way to cluster objects.
## Loading required package: dbscan## I used the kNNdistplot function to determine optimal eps which is at the knee of the graph. I approximated that point to be around 800,000 as this part can vary depending on who looks at the graph. If the knee doesn't give you the best results, it's absolutely okay to charge it to an eps that results in better clusters.## While using this method you need to make sure your data is numeric this can be done with the following functions:
## nums=unlist(lapply(data,is.numeric))
## data=data[,nums]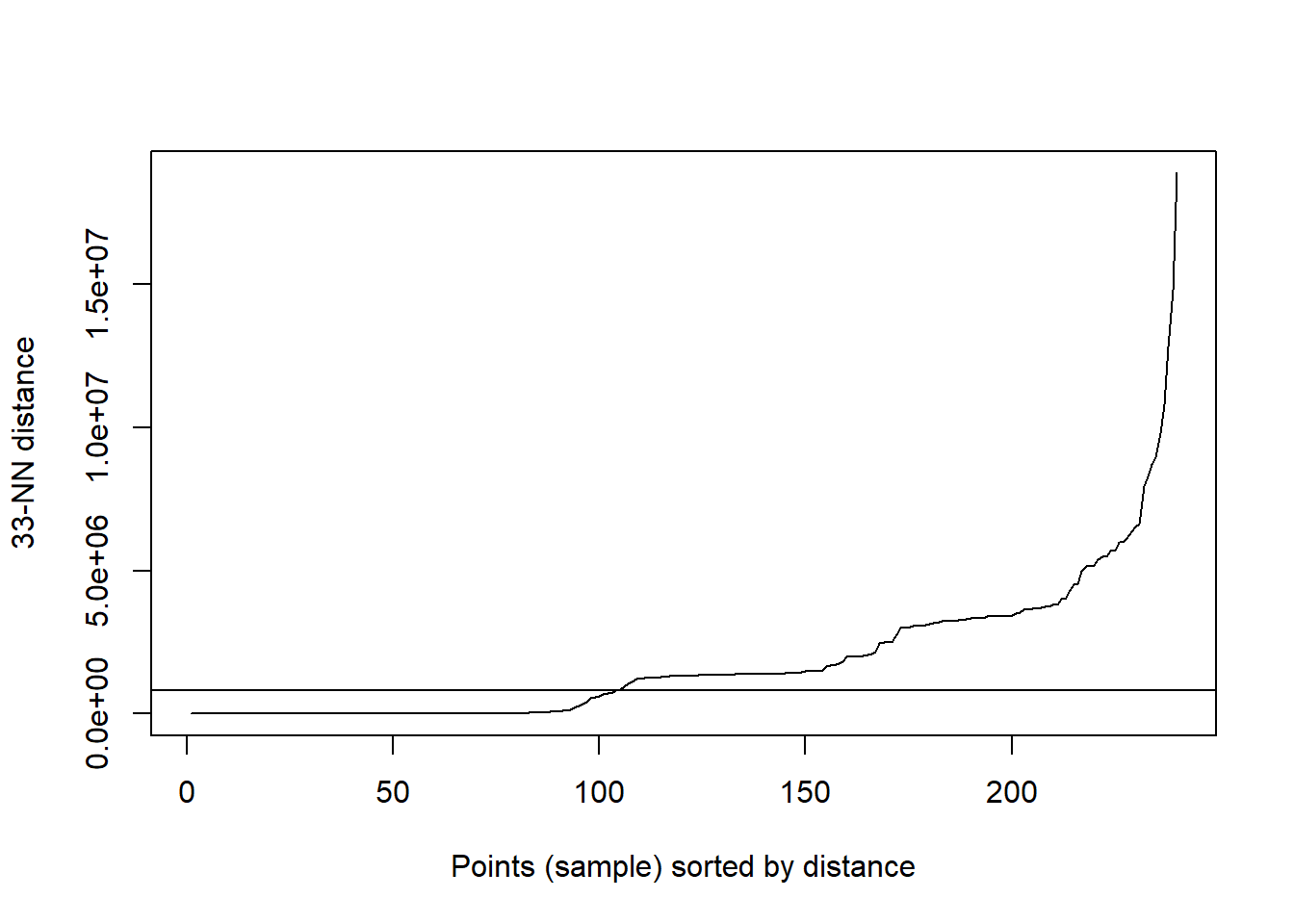
## integer(0)## DBSCAN clustering for 240 objects.
## Parameters: eps = 8e+05, minPts = 5
## The clustering contains 4 cluster(s) and 9 noise points.
##
## 0 1 2 3 4
## 9 15 179 15 22
##
## Available fields: cluster, eps, minPts## [1] 0 0 1 0 0 2 3 3 2 3 1 3 2 2 1 2 2 3 4 1 1 3 0 2 2 1 1 3 1 3 2 1 3 2 2 2 2
## [38] 3 2 0 4 2 4 3 4 2 2 3 4 4 2 0 1 1 4 2 4 4 2 2 2 2 2 4 2 2 3 2 2 2 1 2 1 2
## [75] 2 4 4 2 4 2 2 2 2 0 2 4 3 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 1 2 2 3 2 4 2 2
## [112] 4 2 2 2 2 2 2 2 4 2 2 2 2 4 4 2 4 2 2 2 2 4 2 2 2 2 2 2 2 2 4 2 2 2 2 2 2
## [149] 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
## [186] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
## [223] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2Post-Analysis
This is 100% the most important part of clustering because until now we have learned nothing besides how the data was split up. Now we need to figure out why, as well as how the different clusters compare? You could easily just output the summary statistics of each cluster and get a decent idea of what objects each cluster consists of but that’s boring so I’ll show you with visuals instead. I will only be performing the post-analysis on the Hiearchical Clustering technique because I believe it performed better simply by looking at which points were clustered where. However there are methods to evaluating which clustering technique performed the best but they aren’t widely known. You could use silhouette coefficients, gap statistics, or the NbClust package in R. I am not going to go further into those but it should be noted that there are ways to evaluate how well your data was clustered. Also there are ways to determine the optimal amount of clusters for techniques like hierarchical clustering or kmeans by looking at the total within sum of squares or the between sum of squares divided by the total sum of squares but I didn’t show that as it’s not tremendously important.
Cluster analysis isn’t about looking at every cluster though because you would then just be looking at the entire data set once again. I compared the clustering method to the salary prediction on the regression models page to get an ideal of which clusters had the players that you would want on your team. As you can see from the plots above cluster 1, which is rather small, consists of the outliers who are Albert Pujols, Mike Trout, and Miguel Cabrera. Obviously not everyone will agree but I would never have them on my team as they are way too costly. Cluster 2 looks to have players that are overpaid strictly due to their age because age was a giant predictor of how much a player should be paid. Cluster 3 is my favorite cluster because I believe if a team wants to save money and get a good appreciating prospect they are going to be in cluster 3. It consists of younger players that are usually predicted to be paid more than they are earning. Obviously you aren’t just going to simply select a player because a machine told you that they were in the 3rd cluster. I do believe you should look at players in this cluster first though before moving to other clusters depending on needs. If you want a cheap young player that will add surplus value to your team cluster 3 is where you should look. I could very easily make a plot showing who is in cluster 3 but I believe this is valuable information. If a MLB team or individual would like to pay for the information I would be happy to negotiate. My email is jtvance@butler.edu.
After further analysis you can see that the machine grouped all of the very cheap players in cluster 3. The more expensive older players that would have been in cluster 3 if I used four groups are in cluster 5. I would not have every player on my team from the 3rd cluster. A team definitely needs a couple cluster 5 players that will still add surplus value but will also add experience because older players aren’t paid more for absolutely no reason. With that said looking for undervalued older players is important because teams like the giants who have an average age of 32 are paying so much extra just for experience that isn’t helping them win games. I also showed the average homeruns for all the players in each cluster to show on a basic level that the player’s performance between all the clusters don’t vary a tremendous amount.